Cryptocurrency Indices
Diversification mitigates risk and improves returns. Studies found that 95% of active traders fail to beat the index. We built the HODL indices for users who want to diversify across the market instead of picking individual coins.


Customized Portfolios
Select any coins, choose a weighting strategy, and see how it performed in the past. Use advanced market metrics to construct dynamic portfolios. You can also create a cryptocurrency index comprised of the top N coins.
Automatic Rebalancing
When the market shifts, a portfolio will drift away from its target allocation. HodlBot automatically rebalances your portfolio to keep it on track, saving you time. Portfolio rebalances generally lead to risk mitigation and improved returns.
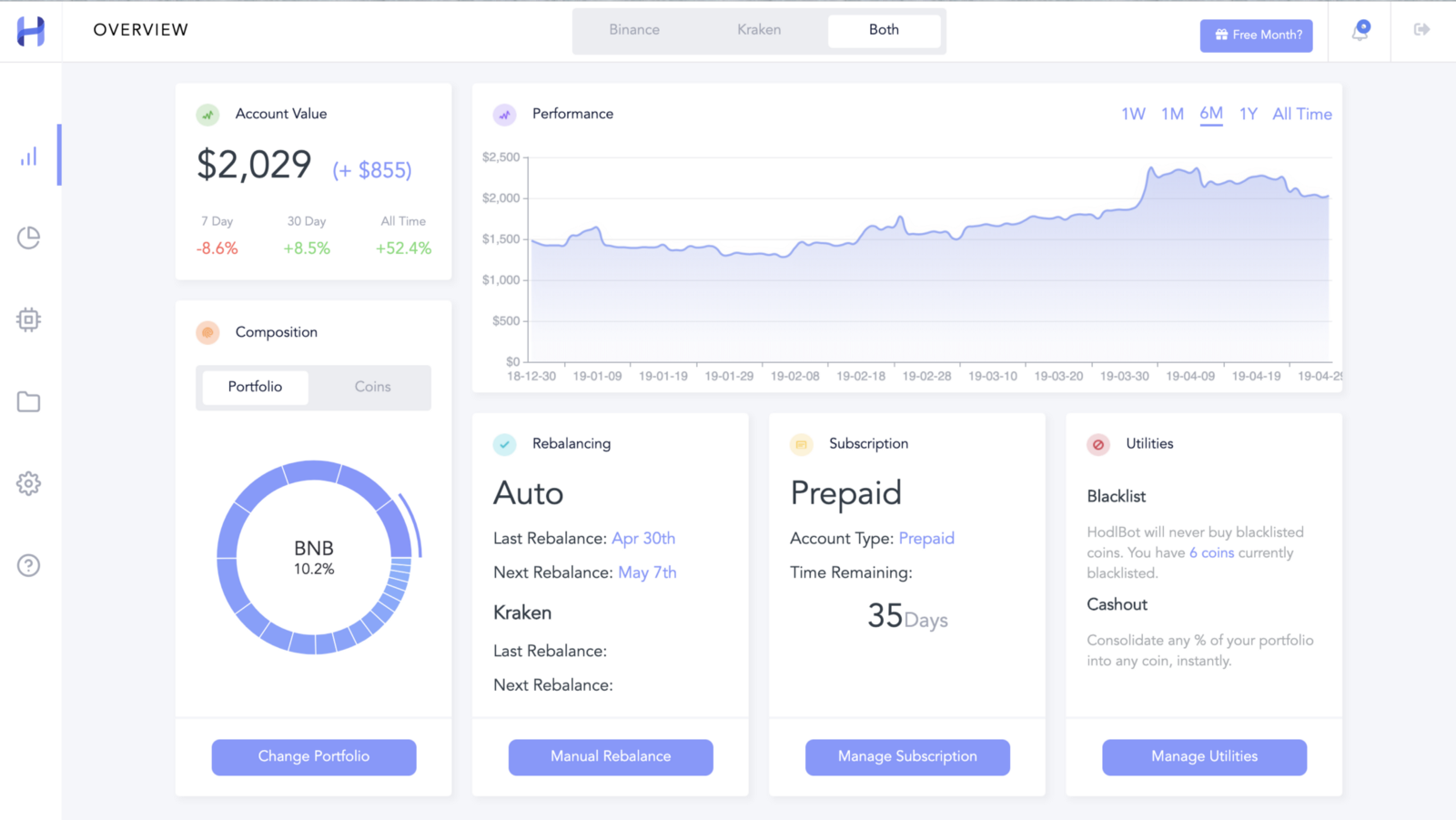
Tailored to Your Needs
Change your rebalancing frequency, blacklist coins you want to avoid trading, liquidate your assets anytime. HodlBot is highly customizable. On top of that, we provide 24/7 customer support.